Mathematische Skulptur

Rinus Roelofs (*1954 Sleen / Niederlande, lebt und arbeitet
in Hengelo): Ring Polyhedra - Twisted Rings (2010)

Nylon, Sinter-3D-Druck, ca. 10 cm Durchmesser.

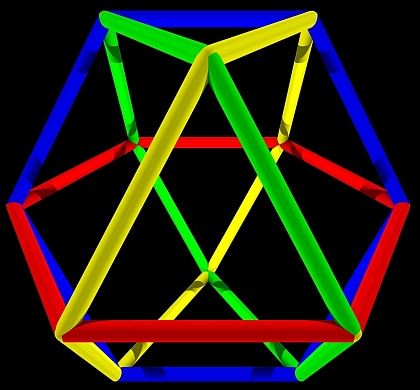
Das Design entspricht einer Zerlegung der 24 Kanten des Kuboktaeders
in 4 gleichseitige Sechsecke (im Bild farbig):

Die Kreuzungen (an denen ein Band durch einen Schlitz in einem anderen Band geführt wird) entsprechen den 12 Ecken des Kuboktaeders; die verdrillten Bänder entsprechen den Sechsecken. Ein Kuboktaeder hat 14 Seiten(flächen): 6 Quadrate und 8 regelmäßige Dreiecke. In jeder Ecke treffen genau zwei Dreiecke und zwei Quadrate aufeinander. Da die Ecken ununterscheidbar sind, zählt der Kuboktaeder zu den 13 archimedischen Körpern.

Anmerkung: Kuboktaeder ist ein Kofferwort aus Kubus (Würfel) und Oktaeder. Dies rührt daher, dass man jeweils den Kuboktaeder erhält, wenn man die Ecken des Würfels bzw. des Oktaeders bis zum Mittelpunkt der Kanten abstumpft.

[Grafik: Wikimedia Commons]

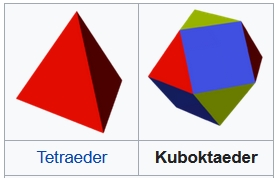
Auch mit dem Tetraeder ist der Kuboktaeder geometrisch eng verwandt:

[Grafik: Wikimedia Commons]

Man erhält den Kuboktaeder aus dem Tetraeder, indem man dessen 6 Kanten genau so viel abstumpft, dass die neu entstehenden 4 Dreiecke (grün) genauso groß sind wie der Rest, der von den 4 (roten) Dreiecksseiten verbleibt. Anstelle der 6 Kanten des Tetraeders hat der Kuboktaeder nun 6 Quadrate (blau).