Mathematische Skulptur

Bathsheba Grossman (*1966, lebt und arbeitet nahe Boston):
Quintrino (2004)

Quintrino hat die Symmetrie des Dodekaeders.

Es gibt zwei Ansätze, um das Design von Quintrino zu verstehen. Ein guter Ausgangspunkt ist das Fußball-Polyeder (Ikosaederstumpf): seine Oberfläche besteht aus 12 regelmäßigen Fünfecken (schwarz im Bild) und 20 regelmäßigen Sechsecken (weiß).

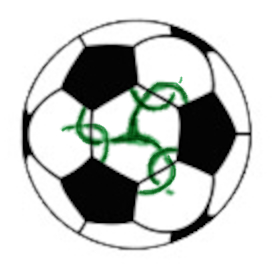
Die Kanten, die die regelmäßigen Fünfecke des Ikosaederstumpfs verbinden, werden ersetzt durch zwei Arme (grün im Bild), die um einander herum ins Innere der Skulptur geführt werden. Dort vereinen sich unter einem weißen Sechseck jeweils drei Arme zu einem Wirbel in Form eines dreiendigen Bumerangs.

Vom Dodekaeder ausgehend, lässt sich das Design von Quintrino nun wie folgt interpretieren: die regelmäßigen Fünfecke des Dodekaeders werden geschrumpft; an den Stellen, an denen die Ecken des Dodekaeders lagen (wo drei Fünfecke zusammenstießen), platziere man die dreiarmigen Wirbel; die Arme der Wirbel korrespondieren dabei mit den Kanten des Dodekaeders; dort, wo ehedem eine Kante zwei Fünfecke verband, appliziere man an jedem der beiden anliegenden Fünfecke einen Arm, der zum anderen Fünfeck hinüberreicht, der jedoch auf halben Weg ins Innere der Skulptur abtaucht: zum Wirbel hin. Unter jeder ehemaligen Dodekaeder-Kante entsteht auf diese Weise ein Loch, durch das man durch Quintrino hindurchsehen kann.

Mehr: [ bathsheba.com, mit Animationen ]
sowie [ Paul Nylander: Knotted Surface ] [ Grossmans erste Skulptur nach diesem Konzept war Ora mit der Tetraedergruppe als Symmetriegruppe. Sie entstand in den frühen 1990er Jahren. ]