 Mathematische Skulptur
Mathematische Skulptur

|

|

|
Friedhelm Kürpig
(*1942 Düsseldorf, lebt und arbeitet in Aachen):
3 Varianten eines Ikosaeders (2011)
Edelstahlblech, 228 mm Durchmesser (Umkugel).
Mit seinen "slice-form-Polyedern" hat Kürpig eine Darstellungsform gefunden, die die Symmetrieeigenschaften dieser geometrischen Körper in den Blick rückt. Die Skulpturen dieser Werkreihe sind ähnlich konstruiert: zu einem gegebenen geometrischen Körper (genauer: regulären Polyeder) wird eine Symmetrieachse (durch eine Ecke, eine Kante oder eine Seitenmitte) gewählt. Gedanklich wird das Polyeder sodann jeweils orthogonal zu dieser Symmetrieachse in dünne "Scheiben" geschnitten - es entstehen lauter regelmäßige Vielecke. Kürpig konstruiert zunächst eine Reihe dieser Schnittflächen - also regelmäßige Vielecke - exakt, dann schneidet er sie mit einem Laser aus 1.2 mm starkem Edelstahlblech aus. Mittels passgenauer Distanzstücke werden die Bleche schließlich parallel (und für das Auge äquidistant) an einer Achse montiert. Weil die Schnittflächen - die regelmäßigen Vielecke - dieselbe Drehsymmetrie wie der betrachtete Polyeder bezüglich der gewählten Drehachse besitzen, veranschaulicht ein "slice-form-Polyeder" in besonderer Weise jeweils eine bestimmte Drehsymmetrie des Polyeders.
Für das Ikosaeder schuf Kürpig entsprechend eine Serie aus drei Varianten, denn das Ikosaeder besitzt drei Drehsymmetrien: über den Kanten eine 2-zählige Drehsymmetrie, über den Seitenflächen eine 3-zählige Drehsymmetrie sowie über den Ecken eine 5-zählige Drehsymmetrie. Das heißt, eine Drehung um eine halbe Volldrehung (180°) bzw. eine Drittel Volldrehung (120°) bzw. eine Fünftel Volldrehung (72°) um die jeweilige Körperachse (s. Abbildung) überführt das Ikosaeder wieder in sich selbst:
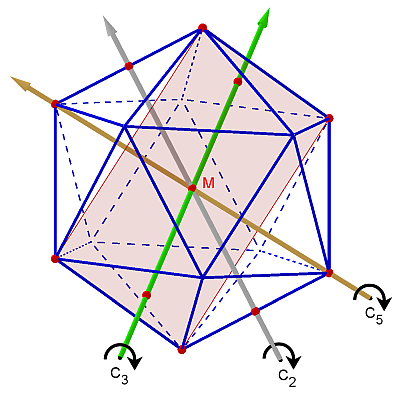
[Abbildung: Wikimedia Commons]
Die oben abgebildete Variante des Ikosaeders verdeutlicht seine 2-zählige Drehsymmetrie. Die Drehachse, an der alle Bleche befestigt sind, durchsticht eine seiner Kanten mittig.
Über den Künstler. Kürpig erlernte zunächst das Schreinerhandwerk. Anschließend absolvierte er ein Studium der Architektur an der RWTH Aachen. Im Rahmen seiner sechsjährigen Tätigkeit als wissenschaftlicher Assistent am Institut für Geometrie und Praktische Mathematik der RWTH Aachen entwickelte er viele Modelle für den Unterricht in Darstellender Geometrie, bevorzugt noch in Holz und Papier. 1975 übernahm Kürpig Herstellung und Vertrieb der Modellserie “Mathematische Modelle Darmstadt” und arbeitete sodann freiberuflich. Die Modelle erforderten Metallverarbeitung in hoher Präzision, diese eignete er sich autodidaktisch an. Eine Professur für Konstruktive Geometrie führte Kürpig von 1984 bis 2007 an die Hochschule für Bildende Künste Hamburg. Eine Ausstattung des Instituts mit CAD-Software in Kombination mit einem numerisch gesteuerten Laser, mit dem sich Edelstahlbleche schneiden ließen, gab der Entwicklung von Modellen 2002 neue Impulse: Wie kann die Ästhetik eines Modells für den Verstehensprozess didaktisch nutzbar gemacht werden? Kürpig leistete auf den Tagungen der Deutschen Gesellschaft für Geometrie und Grafik (DGfGG) regelmäßig Fachbeiträge und war dort auch als Herausgeber tätig. Seine "slice-Polyeder" stellte er erstmals im Frühjahr 2011 auf der Jahrestagung der DGfGG an der TU Dresden vor (3 Varianten des Dodekaeders). Einzelausstellungen richteten Kürpig u.a. ein: 2000 die RWTH Aachen (anlässlich einer Tagung der Deutschen Gesellschaft für Kristallographie) sowie 2005 die Leibniz Universität Hannover (anlässlich der 1. Jahrestagung der Deutschen Gesellschaft für Geometrie und Grafik). Das mathematikum, Gießen, widmete Kürpig 2012 eine große Einzelausstellung, ebenso 2019 (gemeinsam mit Koos Verhoeff).
Historische Einordnung. Volumenmodelle von von regulären Polyedern konnten schon in der Antike aus Holz oder Stein gestellt werden. Je nach Zweck sind andere Visualisierungen besser geeignet. Kürpigs Konzept der "slice-Polyeder" sind in einer historischen Linie zu sehen mit:
1. den Kantenmodellen ("Körpergerüst") von Leonardo da Vinci (1452-1519), mit denen er Luca Paciolis Buch The Divine Proportion (1509) illustrierte. Erstmals erlaubten sie, alle Kanten und Ecken gleichzeitig in den Blick zu nehmen, wobei die räumliche Anordnung (was ist vorne, was ist hinten?) klar erkennbar ist. Der Fokus verschiebt sich weg von den Flächen hin zur kombinatorischen Struktur unter den Ecken und Kanten. Im Unterricht können solche Modelle heute aus magnetischen Metallstiften und -kugeln baut werden (vgl. GeoMag).
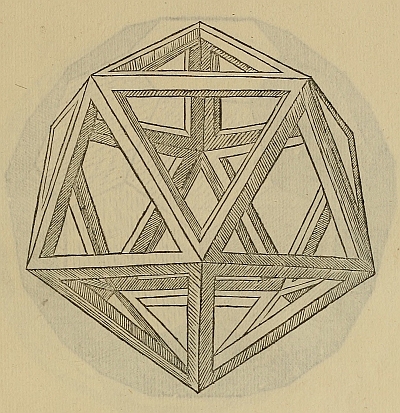
[Foto: Wikimedia Commons]
2. den Körpernetzen, bei denen die Seitenflächen eines geometrischen Körpers in die Ebene abgewickelt werden. Sie sind bei der Berechnung des Flächeninhalts der Körperoberfläche ebenso dienlich wie als Vorlage für die Erstellung von Körpermodellen durch Falten. Körpernetze gehen auf Albrecht Dürer (*1471 Nürnberg †1528 ebd.) zurück [Vnderweysung der messung mit dem zirckel und richtscheyt in Linien ebnen unnd gantzen corporen, 1525].

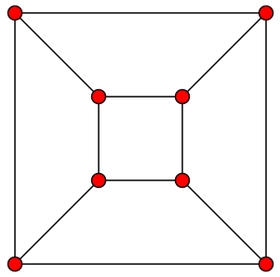
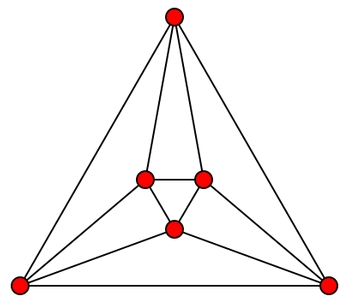
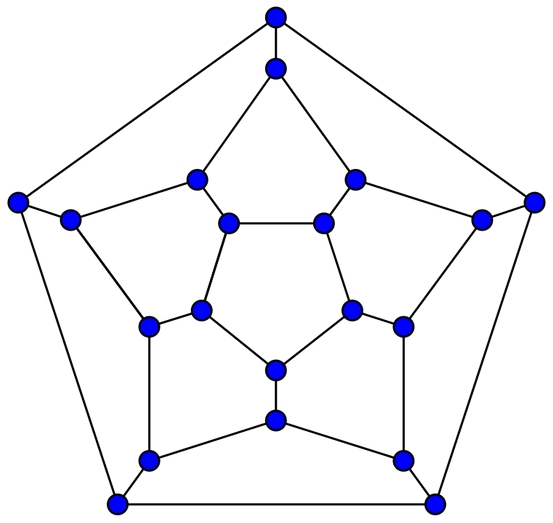
3. Der Schlegel-Graph (nach Victor Schlegel, 1843–1905) abstrahiert von Volumen, Längen und Winkeln des Polyeders, er zeigt lediglich noch, wie Ecken und Kanten zueinander stehen ("topologische Eigenschaften"). Man kann sich den Schlegel-Graph als Projektion des Körpergerüsts in die Ebene vorstellen [Victor Schlegel: Theorie der homogen zusammengesetzten Raumgebilde. Nova Acta Leop. Carol. XLIV (4), 1883]. Er eignet sich besonders für die Untersuchung kombinatorischer und algorithmischer Fragestellungen wie z.B. Färbungen, Hamiltonkreis oder Euler-Zyklus.


[Foto Skulpturen: mit freundlicher Erlaubnis © Friedhelm Kürpig]