Mathematische Skulptur

Friedhelm Kürpig (*1942 Düsseldorf, lebt und arbeitet in Aachen):
Tetraeder (2015)

Edelstahlbleche, 8 mm bzw. 20 mm stark, lasergestrahlt. Länge der Tetraederkanten: 160 cm, knapp 1.5 t schwer. Standort: Mathematikum, Liebigstraße 8, Gießen; im März 2015 aufgestellt.

Der Tetraeder ist für die meisten von uns ein sehr ungewohnter geometrischer Körper. Am ehesten kennen wir ihn: liegend.

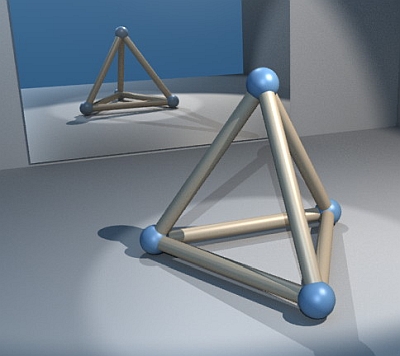
[Foto: Wikimedia Commons]

In dieser Position - mit einer Ecke nach oben - erscheint der Tetraeder als eine dreiseitige Pyramide. Entsprechend vertraut ist uns seine 3-zählige Rotationssymmetrie: jede Drittel-Volldrehung um die Achse senkrecht durch eine Seitenmitte (sowie die gegenüberliegende Ecke) führt den Körper wieder in sich selbst über.

Kürpig hingegen stellt das Tetraeder - wie es 1619 schon Johannes Kepler in seinem Werk Harmonices Mundi (V) (zu Deutsch: Weltharmonik) tat - auf eine Kante:

Johannes Kepler entdeckte, dass das Tetraeder in einen Würfel
einbeschrieben werden kann. [Abbildung: Wikimedia Commons]

Die Edelstahlbleche in Kürpigs Tetraeder entwickeln sich von einem lang gezogenen rechteckigen, von unten nach oben verlaufenden Blech (ganz links im Foto) zu einem wiederum rechteckigen, aber von oben nach unten verlaufenden Blech (ganz rechts im Bild). Das rechte ist dabei im Verhältnis zum linken um genau 90° gedreht. Kürpigs Tetraeder macht auf die 2-zähligen Symmetrien des Tetraeders aufmerksam: auch halbe Volldrehungen um die (drei) Achsen, die gegenüberliegende Kanten mittig schneiden, führen das Tetraeder wieder in sich selbst über:

[Foto: Wikimedia Commons]

Genau entlang einer solchen Achse hat Kürpig denn auch die Bleche seiner Skulptur "aufgehängt".